Shuffling 的算法艺术

Posted 昨天 Updated 昨天

By abing

8~11 min read

牌类游戏，自古到今都有各种变型，从三国杀、炉石到斗地主以及更久远的德州，这些卡牌游戏永远都绕不开一个问题——洗牌。而洗牌的本质，就是让牌的每个排列出现的概率相等。我们现实中要实现基础的随机化洗牌自然容易，当然，魔术师也会使用各种方法，来诱导你相信，他们的洗牌是 “公平” 的。那么对于计算机来说，我们如何保证各类棋牌游戏中，洗牌的公平与随机呢？这就是今天要阐述的课题。

公平的数学基础

刚刚我们提到了洗牌如果需要公平，那就得让牌的每个排列出现的概率相等，换句话说，每个排列都得 “可能” 出现相同的次数，这就是我们所说的 “期望” 。举个例子，当我们手上有「9、10、J」三张牌的时候，我们可能的组合，就有如下几种：

「9、10、J」，「9、J、10」
「10、9、J」，「10、J、9」
「J、10、9」，「J、9、10」

换个理解的方式，我们第一个位置可以有「3」张卡牌可以选择，但是选择其一，第二次的时候，我们便只有「2」张卡牌可以供选择了，到最后，只剩下「1」张卡牌能够选择，因此总的排列数量就是「3 ✖️ 2 ✖️ 1」一共「6」种。换成4张牌的时候，我们同样可以根据这个方法算出一共有「24」种排列。

而我们的目的，就是让这每种排列出现的概率相等。

朴素的洗牌

按照我们上述朴素的想法，我们可以很快的写出对应的代码：

function originalFisherYates(arr) {
  const result = [];
  const src = arr.slice();

  while (src.length > 0) {
    const idx = Math.floor(Math.random() * src.length);
    result.push(src.splice(idx, 1)[0]);
  }

  return result;
}

上述代码在概率学上，确实做到了各种排列出现的概率一致，但是对于计算机来说——它太慢了，注意到src.splice(idx, 1) 这个，从原数组中踢出所随机出来的这个元素，其实时间复杂度是O(n) 的，而我们又要遍历整个原数组一遍，因此对于整体而言，它的时间复杂度，实际上是O(N^2) 。对于动辄几百上千的数据来说，这个时间复杂度，是我们没办法承受的，因此，我们必须要做出改进。

改进后的 Fisher-Yates

到了 1964 年，Durstenfeld 对它进行了原地优化（即就地打乱，无需新数组）：

function fisherYates(arr) {
  const result = arr.slice();

  for (let i = result.length - 1; i > 0; i--) {
    const j = Math.floor(Math.random() * (i + 1)); // 0 <= j <= i
    [result[i], result[j]] = [result[j], result[i]];
  }

  return result;
}

上述的代码中，我们倒叙遍历数组，每次从[0, i] 中选出一个，与当前位置交换。

但是比较绕的是，为什么就地打乱，也可以做到同样的效果呢？他在数学上是正确的？那就让我们来证明一下。

第一步，当 i = n - 1 的情况下：

从下标 j ∈ [0, n − 1] 中随机选一个，交换到末尾；
被选中放到最后一个位置的元素有 1 / n 的概率

第二步，当 i = n - 2 的情况下：

从剩下的前 n − 1 个元素中随机选一个，放到倒数第二个位置；
被选中元素的概率为 1 / n - 1；
所以前两步组合起来，每个元素排在某个位置的联合概率是 1 / (n - 1) * 1 / n

……

第 k 步，当 i = n - k 当情况下：

从 n − k + 1 个还未“固定”的元素中，等概率选一个放在第 n − k 个位置；
概率是 1 / n - k + 1。

……

所以到最后，我们只剩下一张牌可以选择，因此，所有的步骤组合起来，每个元素排在某个位置的联合概率（即某个组合出现的概率）为：

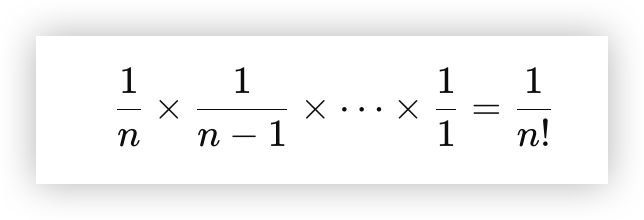
这样子一来，我们在数学上也证明了其正确性。

总结

Fisher-Yates 在改进后，现代 Fisher–Yates 洗牌算法在每一步中都以等概率做选择，且每一步选择独立，最终能等概率地产生所有 n! 个排列。

License: CC BY 4.0