鸟群算法 Boids

Posted recently Updated recently

By abing

17~22 min read

Boids 鸟群算法，全称 brid-oid object，类鸟对象，最近偶然看到，感觉挺有意思的，简单的三条规则组成的系统，就能够模拟自然中大量动物的群聚行为，确实有其瑰丽所在。

从它的三条核心规则开始说起，克雷格·雷诺兹 Craig Reynolds 从观测群聚动物的过程中发现了群聚动物的行为有以下三个特征：

分离 (Separation): 移动以避免拥挤整个集体 (steer to avoid crowding local flockmates)
对齐 (Alignment): 朝着周围同伴移动的平均方向移动 (steer towards the average heading of local flockmates)
聚集 (Cohesion): 朝着周围同伴的平均位置（质心）移动 (steer to move toward the average position of local flockmates)

把这三条规则，具象为三条影响方向的向量，我们通过计算其每条向量对原速度的影响，就可以得出我们下一个时刻的速度。接下来，我们来一条条详细讲讲对应的实现以及其的数学原理。

行动规则

分离

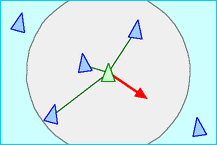
分离行为的目的是移动以避免拥挤整个集体，如果群体内的其他个体过于靠近自己（距离小于自己不爽的范围，下文称之为分离半径 SEPARATION_RADIUS），那么自己就要向着它的反方向进行移动

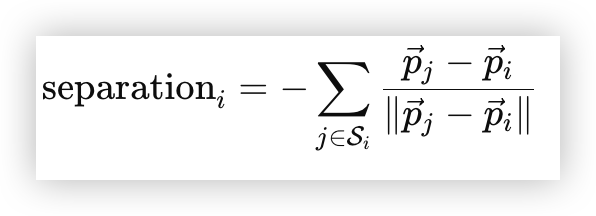
上述公式中，separation 代表的是分离的速度向量，而 S_i 代表的则是在分离半径之内的邻居，p_i 代表的则是每个个体的移动速度。

这样子我们可以很明确知道，距离越近，我们就会越远离对应的个体，反之，距离越远则影响越小。

对齐

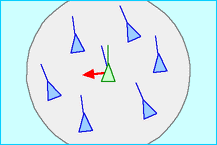
对齐行为的目的是让自己的速度靠近邻居速度的平均值，所以在我们观测得到的半径内，我们都会朝着观察得到的邻居的平均方向进行靠近

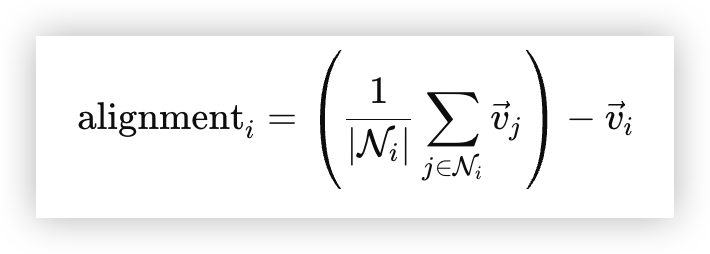
上述公式中，alignment_i代表的是其平均移动方向向量，其实际上是计算观察半径内所有邻居移动的平均方向，减去当前速度，那么就是自身需要向群体对齐的移动方向。

聚集

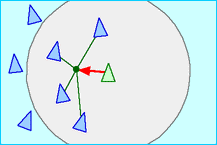
聚合行为的目的是靠近邻居的平均位置，所以，在观测半径内，自身就会朝着这些邻居的平均位置进行靠近

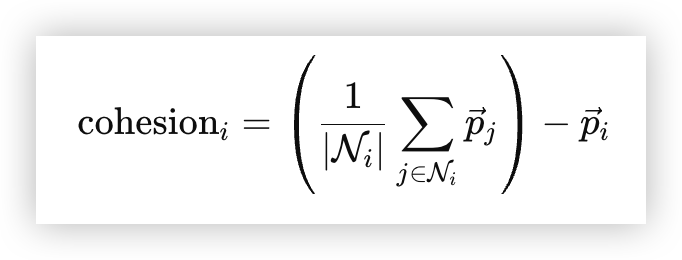
上述公式中，我们计算了观测半径内的邻居的质心，再将其减去自身位置，就可以得出自身聚集行为需要移动的对应向量。

参数

为控制每种行为对个体的影响，因此为每个行动规则都赋予对应的权值。所以有对应如下三个参数：

ALIGNMENT_WEIGHT
COHESION_WEIGHT
SEPARATION_WEIGHT

同时，还有每个个体的观测半径和分离半径：

NEIGHBOR_RADIUS
SEPARATION_RADIUS

最终，为了控制我们的画面，我们还需要规定画布的范围，以及我们所有个体的总数量，并且对每个个体的最大速度加以限制：

NUM_BOIDS
WIDTH, HEIGHT
MAX_SPEED

这样子，通过控制每个参数的行为，我们就可以在宏观上限制整个集体的一些行为。

结果展示

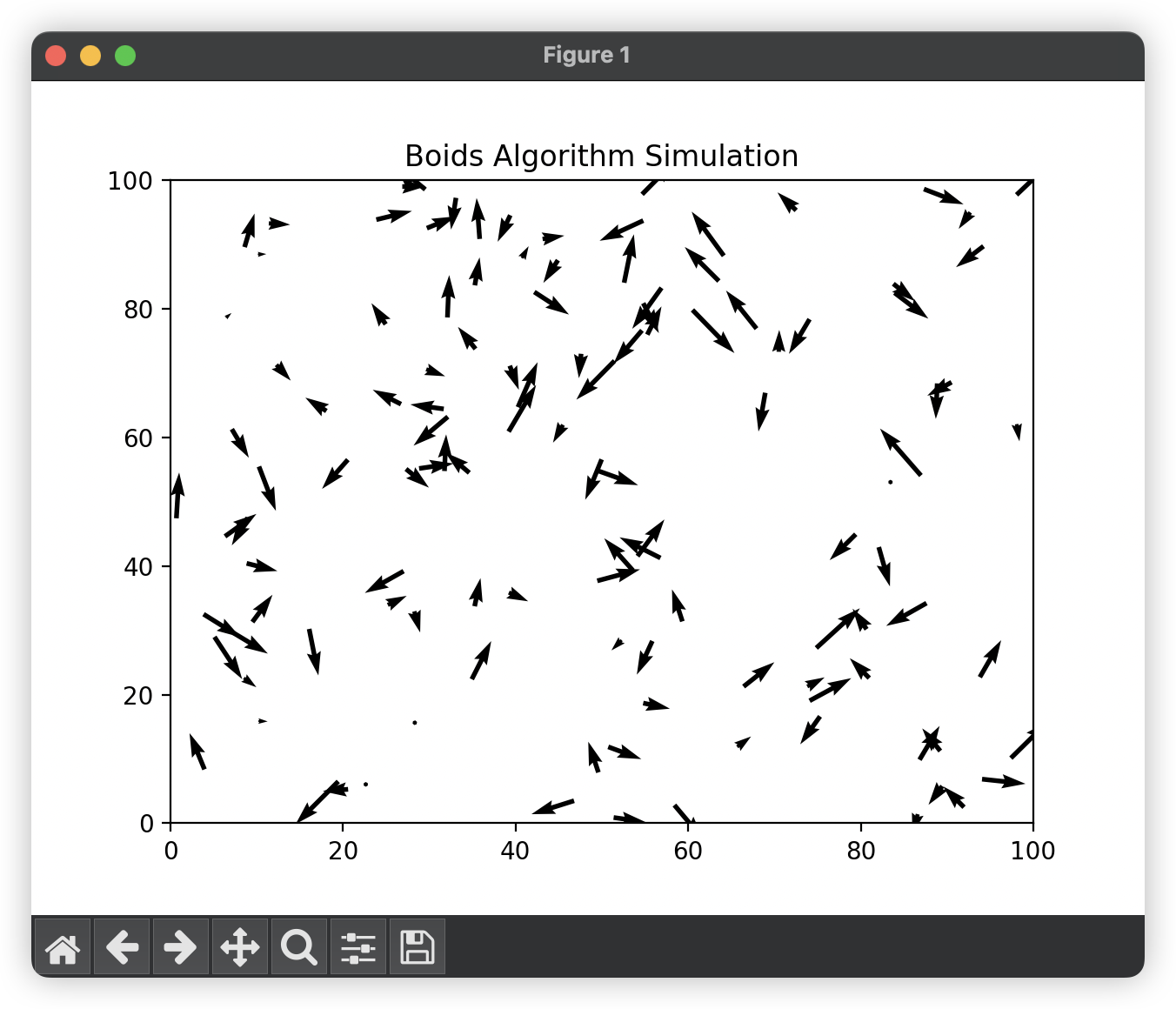
可以看到，上述的各个个体行为一开始都较为混乱

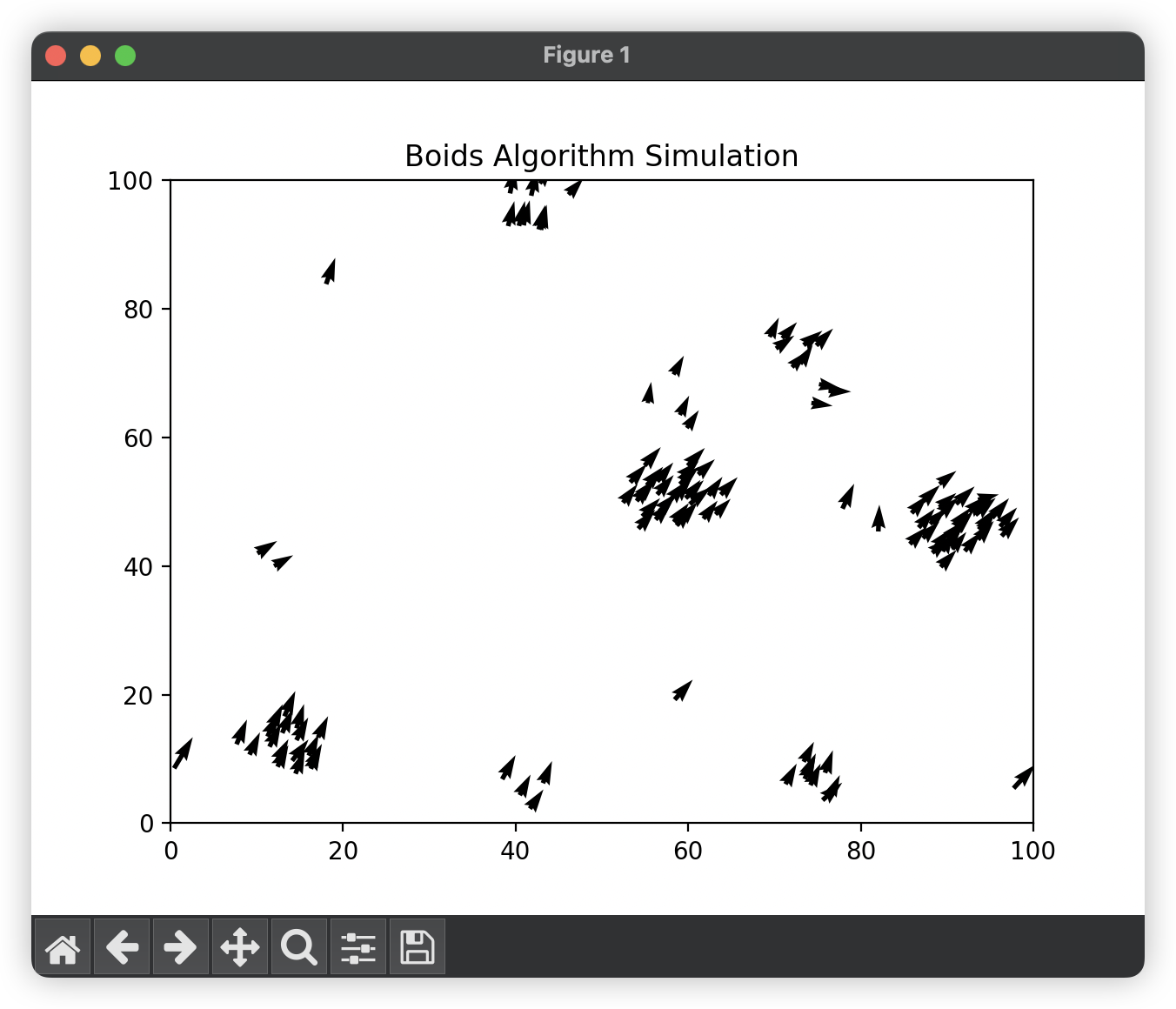
但随着时间的流逝，个体就逐渐被群体所裹挟着前进了。

代码参考

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

# 参数设置
NUM_BOIDS = 120
WIDTH, HEIGHT = 100, 100
MAX_SPEED = 30
NEIGHBOR_RADIUS = 10
SEPARATION_RADIUS = 4
ALIGNMENT_WEIGHT = 0.05
COHESION_WEIGHT = 0.01
SEPARATION_WEIGHT = 0.1

# 初始化 boids
positions = np.random.rand(NUM_BOIDS, 2) * [WIDTH, HEIGHT]
velocities = (np.random.rand(NUM_BOIDS, 2) - 0.5) * MAX_SPEED


def limit_speed(v, max_speed):
    speed = np.linalg.norm(v)
    if speed > max_speed:
        return v / speed * max_speed
    return v


def update_boids():
    global positions, velocities
    new_velocities = np.zeros_like(velocities)

    for i in range(NUM_BOIDS):
        pos_i = positions[i]
        vel_i = velocities[i]

        # 初始化三个行为向量
        # 方向对齐
        alignment = np.zeros(2)
        # 群体聚合
        cohesion = np.zeros(2)
        # 保持距离
        separation = np.zeros(2)
        count = 0

        # 计算邻居的影响
        for j in range(NUM_BOIDS):
            if i == j:
                continue
            offset = positions[j] - pos_i
            distance = np.linalg.norm(offset)
            if distance < NEIGHBOR_RADIUS:
                alignment += velocities[j]
                cohesion += positions[j]
                if distance < SEPARATION_RADIUS:
                    separation -= offset / distance
                count += 1

        if count > 0:
            alignment = alignment / count - vel_i
            cohesion = cohesion / count - pos_i

        vel_i += ALIGNMENT_WEIGHT * alignment
        vel_i += COHESION_WEIGHT * cohesion
        vel_i += SEPARATION_WEIGHT * separation
        vel_i = limit_speed(vel_i, MAX_SPEED)
        new_velocities[i] = vel_i

    positions[:] = (positions + new_velocities) % [WIDTH, HEIGHT]
    velocities[:] = new_velocities


fig, ax = plt.subplots()
ax.set_xlim(0, WIDTH)
ax.set_ylim(0, HEIGHT)
ax.set_title("Boids Algorithm Simulation")

quiver = ax.quiver(positions[:, 0], positions[:, 1], velocities[:, 0],
                   velocities[:, 1])


def animate(frame):
    update_boids()
    # 更新
    quiver.set_offsets(positions)
    quiver.set_UVC(velocities[:, 0], velocities[:, 1])
    return quiver,


ani = FuncAnimation(fig, animate, frames=100, interval=100, blit=True)
plt.show()

License: CC BY 4.0